Photospline¶

Detector response to a high-energy physics process is often estimated by Monte Carlo simulation. For purposes of data analysis, the results of this simulation are typically stored in large multi-dimensional histograms, which can quickly become unwieldy in terms of size or numerically problematic due to unfilled bins or interpolation artifacts. Photospline is a library that uses the penalized spline technique to efficiently compute, store, and evaluate B-spline representations of such tables.

Fitting tutorial (Python)¶

A basic fitting script starts with a few imports:

import numpy
from photospline import glam_fit, ndsparse, bspline

Some of these are strictly required.

numpy - We need this in order to pass n-dimensional arrays around
glam_fit - We will use this to perform a least-squares fit of the spline coefficients to the data.
ndsparse - We will use this sparse N-dimensional grid to pass our data to photospline.glam_fit().

We will also need some extra functions in order to visualize the result.

photospline.splinetable.grideval() - We will use this function to evaluate the spline surface on a coordinate grid.
photospline.bspline() - We will also plot the individual basis functions to get a better idea of how the spline surface is constructed.

For this example, we will make up some random, one-dimensional data drawn from a cosine overlaid on a polynomial:

numpts = 500
x1 = numpy.sort(numpy.random.uniform(-4,25,size=numpts))
z = numpy.random.poisson(numpy.cos(x1)**2 + (x1-3.0)**2 + 10)

We can improve the quality of the fit by giving less weight to data points that are likely to be distorted by statistical fluctuations. Here we’ll use a minimum weight of 1, and weight the high-occupancy points up:

w = 1. + z

Now we need to choose a set of B-spline basis functions. We will use a grid of order-2 B-splines that extend beyond the the data points, relying on the regularization term for extrapolation:

order = 2
penalty_order = order
knots = [numpy.linspace(-8,35,30)]
smooth = 3.14159e3

This generalizes easily to multi-dimensional data; we would simply add an extra entry to knots for each extra dimension.

To actually run the fit, we call photospline.glam_fit():

>>> zs, w = ndsparse.from_data(z, w)
>>> spline = glam_fit(zs,w,[x1],knots,[order],[smooth],[penalty_order])
Calculating penalty matrix...
Calculating spline basis...
Reticulating splines...
        Convolving bases...
                Convolving dimension 0
        Flattening residuals matrix...
Transforming fit array...
Computing least square solution...
Analyze[27]: 0.000049 s
Factorize[27]: 0.000027 s
Solve[27]: 0.000022 s
Done: cleaning up

Now we can save the fit result for later evaluation with photospline.splinetable.write()

spline.write('splinefit-1d.fits')

To see the result, we can plot it with matplotlib:

import pylab
# Plot individual basis splines
xfine = numpy.linspace(knots[0][0], knots[0][-1], 10001)
splines = [numpy.array([bspline(knots[0], x, n, order) for x in xfine]) for n in range(0,len(knots[0])-2-1)]
for n in range(len(splines)):
        pylab.plot(xfine, result.coefficients[n]*splines[n], color=c)
# Plot the spline surface (sum of all the basis functions)
pylab.plot(xfine, spline.grideval([xfine]), label='Spline fit', color='k')
pylab.scatter(x1, z, label='Data')
pylab.legend(loc='upper left')
pylab.show()

The result is shown below:

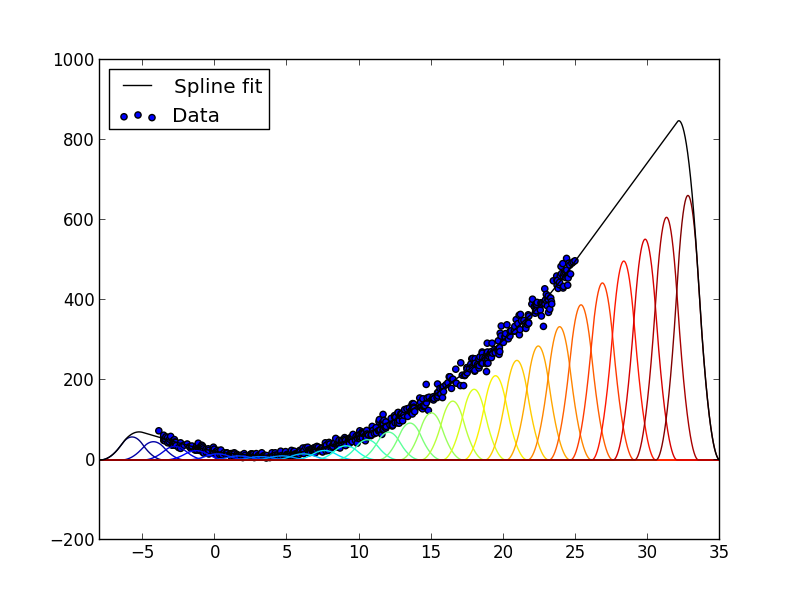
Example 1-dimensional spline fit. The spline surface (black line) is the sum of basis functions (colored lines) weighted with coefficients determined by a linear least-squares fit to the data (blue dots). In the region to the right where there are no data, the order-2 penalty term produces a straight line.¶

Fitting tutorial (C++)¶

We can do the same fit as above in C++. We start with a few necessary includes, namely splinetable and random number generators from the C++11 standard library:

#include <photospline/splinetable.h>
#include <random>

As above, we draw Poisson samples from a cosine overlaid on a polynomial. In contrast to the Python example, though, we fill the data points directly into a sparse array:

std::default_random_engine rng(0);

size_t numpts = 500;
// Create a random coordinate vector
std::vector<double> x1(numpts);
{
        std::uniform_real_distribution<> uniform(-4,25);
        for (unsigned int i=0; i < numpts; i++)
                x1[i] = uniform(rng);
        std::sort(x1.begin(), x1.end());
}
// Create a sparse array to hold the data points and a vector to hold the
// weights. The length of `weights` should be the number of entries in
// `zsparse` with non-zero weights
photospline::ndsparse zsparse(500,1);
std::vector<double> weights(numpts);
for (unsigned int i=0; i < numpts; i++) {
        double z = std::poisson_distribution<>(
            std::pow(std::cos(x1[i]), 2) + std::pow(x1[i]-3.0, 2) + 10)(rng);
        zsparse.insertEntry(z, &i);
        // Use a minimum weight of zero, and weight the high-occupancy points up
        weights[i] = 1. + z;
}

Now, we set up the spline basis and a smoothing coefficient:

std::vector<double> knots(30);
for (unsigned int i=0; i < knots.size(); i++) {
        double lo(-8), hi(35);
        knots[i] = lo + i*(hi-lo)/(knots.size()-1);
}

std::array<uint32_t,1> order = {2};
auto penalty_order = order;
double smooth = 3.14159e3;

Then, run the fit. Since photospline::splinetable::fit() works on N-dimensional data in general, we have to put our knot vector, order, smoothing coefficient, etc. in containers:

photospline::splinetable<> spline;
spline.fit(zsparse, weights, std::array<decltype(x1),1>({x1}), order, {knots}, {smooth}, penalty_order);

Finally, we store the fit result for later use:

spline.write_fits("splinefit-1d.fits");

Python library reference¶

Warning

This needs to be updated to the 2.0 API

The interface to the fitting library is entirely in Python, using Numpy arrays to as containers for the data, spline coefficients, knot vectors, etc. The spline coefficients determined in the fit are stored in FITS files that can be loaded and evaluated using the bundled C library.

Note

The reference Python fitting implementation photospline.glam.glam.fit() uses dense matrix operations from numpy, and can become extremely memory-hungry in large numbers of dimensions.

The C implementation photospline.spglam.fit() implements the same functions as the Python version, but uses sparse matrix operations from SuiteSparse. This is both orders of magnitude faster and uses 100x less memory for typical problems. You should use spglam for large-scale fitting and fall back to glam if necessary for debugging.

photospline.spglam.fit(z, w, coords, knots, order, smooth=1, periods=None, penalties=None, monodim=None)¶: A drop-in replacement for photospline.glam.glam.fit().

photospline.spglam.grideval(table, coords)¶: A drop-in replacement for photospline.glam.glam.grideval().

Note

The bases argument is not supported in this version.

C++ library reference¶

The photospline C++ library provides photospline::splinetable, which represents a tensor-product B-spline surface. These can be fit to data with photospline::splinetable::fit(), written to FITS files with photospline::splinetable::write(), read from FITS files with photospline::splinetable::read(), and evaluated with photospline::splinetable::ndsplineeval().

template<typename Alloc = std::allocator<void>> class photospline::splinetable¶

Public Functions

inline explicit splinetable(allocator_type alloc = Alloc())¶: Construct an empty splinetable. The resulting object is useful only for calling read_fits, read_fits_mem, or fit.

inline explicit splinetable(const std::string &filePath, allocator_type alloc = Alloc())¶

Construct a splinetable from serialized data previously stored in a FITS file.

Parameters: filePath – the path to the input file

inline explicit splinetable(std::vector<splinetable<Alloc>*> tables, std::vector<double> coordinates, int stackOrder = 2, allocator_type alloc = Alloc())¶

Construct a splinetable from stacking other splines.

Parameters

splines – the splines to stack
coordinates – the coordiantes in the stacking dimension of the tables to be stacked
stackOrder – the order of the spline in the stacking dimension

inline bool operator==(const splinetable &other) const¶: Compare splines for equality. Splines are considered equal if evaluation would return the same result at all possible coordinate values. Auxiliary FITS header entries are not considered.

inline bool operator!=(const splinetable &other) const¶: Compare splines for inequality. Splines are considered equal if evaluation would return the same result at all possible coordinate values. Auxiliary FITS header entries are not considered.

bool read_fits(const std::string &path)¶

Read from a FITS file

Parameters: path – the path to the input file

bool read_fits_mem(void *buffer, size_t buffer_size)¶

Read from a FITS ‘file’ in a memory buffer

Parameters

the – input data buffer
buffer_size – the length of the input buffer

void write_fits(const std::string &path) const¶

Write to a FITS file

Parameters: path – the path to the output file

std::pair<void*, size_t> write_fits_mem() const¶

Write to a FITS memory ‘file’.

Returns: A pair containing a buffer allocated by malloc(), which should be deallocated with free(), and the size of that buffer.

inline size_t get_naux_values() const¶: Get the count of ‘auxiliary’ keys.

inline const char *get_aux_key(size_t i) const¶: Directly get a particular auxiliary key.

const char *get_aux_value(const char *key) const¶

Directly get a particular auxiliary value

Parameters: key – the key whose value should be fetched
Returns: the value if key exists, otherwise NULL

bool remove_key(const char *key)¶

Delete an auxiliary key and associated value

Returns: true if the key existed and was removed

template<typename T> bool read_key(const char *key, T &result) const¶

Look up the value associated with an auxiliary key

Parameters

key – the name of the key to look up
result – location to store the value if the key is found

Returns

true if the key was found and the corresponding value was sucessfully parsed into result, otherwise false

bool read_key(const char *key, std::string &result) const¶

Look up the value associated with an auxiliary key

Note

The data extracted may be padded with extra whitespace if it has been read from a FITS file.

Parameters

key – the name of the key to look up
result – location to store the value if the key is found

Returns

true if the key was found

template<typename T> bool write_key(const char *key, const T &value)¶

Insert or overwrite an auxiliary key,value pair

Parameters

key – the name of the key to store
value – the value to store for the key

Returns

whether the value was successfully stored

evaluator get_evaluator() const¶: Constructs an optimized evaluator object which will use the best available internal routines to perform evaulations. The evaluator holds a reference to this splinetable, so it must be considered invalidated if this table altered or destroyed.

bool searchcenters(const double *x, int *centers) const¶

Acquire a centers vector for use with the ndsplineeval functions. This performs a binary search over the knots in each spline dimension, so depending on how the spline was produced a more efficient method may be exist.

Parameters

x – a vector of coordinates at which the spline is to be evaluated
centers – a vector of indices which will be populated by this function

Returns

whether centers was sucessfully populated

Pre

x and centers must both have lengths matching the spline’s dimension

double ndsplineeval(const double *x, const int *centers, int derivatives) const¶

Evaluate the spline hypersurface.

Parameters

x – a vector of coordinates at which the spline is to be evaluated
centers – a vector of knot indices derived from x, constructed using searchcenters
derivatives – a bitmask indicating in which dimensions the spline should be differentiated rather than directly evaluated. Mixed partial derivatives are supported.

Returns

the spline value or derivative value

double operator()(const double *x) const¶

Evaluate the spline hypersurface. This convenience interface for evaluation simply performs searchcenters and ndsplineeval. It assumes that no derivative is desired, and yields zero when searchcenters fails. This is suitable for simple uses where the user knows that the coordinates will be inside the table bounds.

Parameters: x – a vector of coordinates at which the spline is to be evaluated
Returns: the spline value or zero if center lookup fails

double ndsplineeval_deriv(const double *x, const int *centers, const unsigned int *derivatives) const¶

Evaluate arbitrary derivative of the spline hypersurface.

Parameters

x – a vector of coordinates at which the spline is to be evaluated
centers – a vector of knot indices derived from x, constructed using searchcenters
derivatives – a vector giving the order of derivative to compute for each dimension

Returns

the derivative of the spline

void ndsplineeval_gradient(const double *x, const int *centers, double *evaluates) const¶

Evaluate the spline hypersurface and its gradient. If the full gradient is needed along with the spline value this function can be more efficient than repeated calls to ndsplineeval.

Parameters

x – a vector of coordinates at which the spline is to be evaluated
centers – a vector of knot indices derived from x, constructed using searchcenters
evaluates – a vector which will be populated by this function with the spline value, followed by the components of the gradient.

Pre

evaluates must have a length one greater than the dimension of the spline

benchmark_results benchmark_evaluation(size_t trialCount = 1e4, bool verbose = false)¶

Evaluate the spline at random points within the extent

Parameters

trialCountthe – number of times each type of evaluation should be performed. This should be large enough to get a stable result.
verbose – whether the results should be printed to stdout.

void convolve(const uint32_t dim, const double *knots, size_t n_knots)¶

Convolve a single dimension of this spline with another spline. This rewrites the data of this spline in place. The order of the spline will be raised by (n_knots - 1) in the given dimension, i.e. convolving with an order-0 spline (a box function, defined on two knots) will raise the order of the spline surface by 1.

Parameters

dim – the dimension in which the convolution should be done
knots – a vector of positions of the knots of the one dimensional spline used for the convolution
n_knots – the length of knots

inline uint32_t get_ndim() const¶: Get the dimension of the spline.

inline uint32_t get_order(uint32_t dim) const¶: Get the order of the spline in a given dimension.

inline uint64_t get_nknots(uint32_t dim) const¶: Get the number of knots in a given dimension.

inline const double *get_knots(uint32_t dim) const¶: Get the knot vector for a given dimension.

inline double get_knot(uint32_t dim, uint64_t knot) const¶

Get a particular knot from a given dimension

Parameters

dim – the dimension
knot – the index of the knot to fetch

inline double lower_extent(uint32_t dim) const¶: Get the left boundary of the spline in a given dimension.

inline double upper_extent(uint32_t dim) const¶: Get the right boundary of the spline in a given dimension.

inline double get_period(uint32_t dim) const¶: Get the period of the spline in a given dimension.

inline uint64_t get_ncoeffs() const¶: Get the total number of spline coefficients.

inline uint64_t get_ncoeffs(uint32_t dim) const¶: Get the number of coefficients along a given dimension.

inline uint64_t get_stride(uint32_t dim) const¶: Get the stride through the coefficient array corresponding to a given dimension.

inline float *get_coefficients()¶: Raw access to the coefficients. Use with care.

inline const float *get_coefficients() const¶: Raw access to the coefficients.

template<typename DoubleCont, typename UInt32Cont, typename DoubleContCont> void fit(const ::ndsparse &data, const DoubleCont &weights, const DoubleContCont &coordinates, const UInt32Cont &splineOrder, const DoubleContCont &knots, const DoubleCont &smoothing, const UInt32Cont &penaltyOrder, uint32_t monodim = no_monodim, bool verbose = true)¶

Construct an approximating spline for possibly sparse, rectangularly gridded data

Parameters

data – the datapoints to be fit, whose locations are specifed as indices into the coordinates arrays
weights – the relative weights associated with the data points
coordinates – a set of arrays containing the values of the abscissas describing the rectangular grid on which the data points are located
splineOrder – an array of the b-spline orders which the fitted spline should have in each dimension
knots – a set of arrays containing the positions for the knots of the fitted spline in each dimension
smoothing – an array specifying the strength of the regularization to apply in each fit dimension
penaltyOrder – an array specifying the order of the regularization to apply in each fit dimension
monodim – optionally, a single dimension in which the fit should be constrained to be monotonic
verbose – whether to print logging and progress messages to standard output

template<typename DoubleContCont> std::unique_ptr<ndsparse> grideval(const DoubleContCont &coords) const¶

Evaluate the spline on a grid

Parameters: coords – a set of arrays specifying the evaluation points in each dimension

template<size_t N, typename Distribution, typename RNG, typename Transform> std::vector<std::array<double, N>> sample(size_t nresults, size_t burnin, std::array<size_t, N> samplingDimensions, std::vector<double> coordinates, Distribution distribution, RNG &rng, int derivatives, Transform transform) const¶

Draw a number of random samples from the distribution given by a slice through the spline.

Todo:: document parameters

Template Parameters

N – the number of dimensions in which to sample
Distribution – a type which can both evaluate a proposal pdf via double operator()(const std::vector<double>& coordinates) const and can draw samples from that same pdf via std::vector<double> sample(RNG rng)
RNG – a random number generator, conforming to the standard interface
Transform – a callable type which can transform values of the spline, given the vector of coordinates at which the spline was evaluated and the resulting value of the spline surface.
N – the number of dimensions in which to sample
Distribution – a type which can both evaluate a proposal pdf via double operator()(const std::vector<double>& coordinates) const and can draw samples from that same pdf via std::vector<double> sample(RNG rng)
RNG – a random number generator, conforming to the standard interface
Transform –

Parameters

nresults – the number of samples to draw
burnin – the length of the burn in period to use
samplingDimensions – the dimensions in which sampling is to be done
coordinates – vector of coordinate values at which the spline is to be evaluated in the dimensions not being sampled. The length of this vector must be the same as spline dimension, but entries for the sampling dimensions will be ignored.
distribution – the proposal distribution
rng – the source of randomness used for sampling
derivatives – a bitmask indicating in which dimensions the derivative of the spline surface is to be taken rather
transform – the transformation function to apply to the spline suface before sampling. This is useful when one wishes to sample from a distribution, but has created a spline representing a transformed version of the pdf (for example its logarithm), in which case transform should be a function which undoes the transformation which was applied to the create the spline. Alternatively, one may wish to sample from a distribution in the space of some set of variables xi, but have created a spline in the space of some transformed variables xi’, in which case transform should account for the jacobian of the change of variables. A combination of these cases is also possible.

Pre

The entries of coordinates for dimensions which do not appear in samplingDimensions must be with in the extents of spline

Pre

The entries of coordinates for dimensions which do not appear in samplingDimensions must be with in the extents of spline

template<size_t N, typename Distribution, typename RNG> std::vector<std::array<double, N>> sample(size_t nresults, size_t burnin, std::array<size_t, N> samplingDimensions, std::vector<double> coordinates, Distribution distribution, RNG &rng, int derivatives = 0) const¶: A version of sample which does not apply a transformation. See sample for more details.

void permuteDimensions(const std::vector<size_t> &permutation)¶

Reorder the dimensions of the spline

Parameters: permutation – the new order in which the current spline dimensions should appear

Public Static Functions

static size_t estimateMemory(const std::string &filePath, uint32_t n_convolution_knots = 1, uint32_t convolution_dimension = 0)¶

Estimate the memory needed to load an existing spline. This function is intended for users using specialized allocators for which it is useful to know the total memory required before constructing the allocator and splinetable. If a convolution will be applied to the spline after it is loaded, doing so will increase its memory requirements, which this function can also take into account.

Parameters

filePath – the path to the input FITS file
n_convolution_knots – the number of knots possessed by the other spline with which one dimension of this spline will be convolved. A value of one is equivalent to no convolution.
convolution_dimension – the dimension of this spline which will have a convolution applied.

Public Static Attributes

static constexpr uint32_t no_monodim = PHOTOSPLINE_GLAM_NO_MONODIM¶: constant used to specify that no dimension should be forced to be monotonic when fitting.

struct benchmark_results¶

A container for results obtained from benchmark_evaluation.

Public Members

double single_eval_rate¶: The rate at which ndsplineeval can evaluate the value of the spline.

double gradient_single_eval_rate¶: The rate at which ndsplineeval can evaluate the gradient of the spline (requiring a number of calls to ndsplineeval equal to the spline dimension per evaluation)

double gradient_multi_eval_rate¶: The rate at which ndsplineeval_gradient can evaluate the value and gradient of the spline

struct evaluator¶

Manages use of optimized spline evaluation routines.

Particular splines may have properies which can be exploited to evaulate them more efficiently (e.g. having a constant, low order in all dimensions). For technical reasons (primarily the inadvisability of storing function pointers in shared memory) it is best to separate the data about which internal functions have been selected for greatest efficiency from the splinetable object itself. The evaluator type safely encapsulates this information, and presents the same evaluation interface as the splietable itself to users.

Since the evaluator holds a reference to the actual splinetable from which is want obtained it must be considered invalidated if that table is altered or destroyed.

Public Functions

inline const splinetable<Alloc> &get_table() const¶: Get the underlying splinetable.

bool searchcenters(const double *x, int *centers) const¶: same as splinetable::searchcenters

double ndsplineeval(const double *x, const int *centers, int derivatives = 0) const¶: same as splinetable::ndsplineeval

double operator()(const double *x, int derivatives = 0) const¶: Convenince short-cut for ndsplineeval.

void ndsplineeval_gradient(const double *x, const int *centers, double *evaluates) const¶: same as splinetable::ndsplineeval_gradient

double ndsplineeval_deriv(const double *x, const int *centers, const unsigned int *derivatives) const¶: same as splinetable::ndsplineeval_deriv

C library reference¶

The photospline library also provides wrapper functions to create, read, and evaluate photospline::splinetable instances from C.

double ndsplineeval(const struct splinetable *table, const double *x, const int *centers, int derivatives)¶

Evaluate the spline surface at coordinates x, with optional single differentiation

Parameters

[in] x – coordinates at which to evaluate
[in] centers – indices of the central splines
[in] derivatives – bitmask indicating which dimensions to differentiate

Pre

centers has been filled via a call to tablesearchcenters()

Returns

the value of the spline surface (or one of its derivatives) at x

int splinetable_glamfit(struct splinetable *table, const struct ndsparse *data, const double *weights, const double *const *coords, const uint32_t *splineOrder, const double *const *knots, const uint64_t *nknots, const double *smoothing, const uint32_t *penaltyOrder, uint32_t monodim, bool verbose)¶

Spline table I/O and manipulation¶

int splinetable_init(struct splinetable *table)¶: Construct a new spline table.

int readsplinefitstable(const char *path, struct splinetable *table)¶: Read a table from a FITS file on disk.

int writesplinefitstable(const char *path, const struct splinetable *table)¶: Write the table to a FITS file on disk.

int writesplinefitstable_mem(struct splinetable_buffer *buffer, const struct splinetable *table)¶: Write the table to a FITS ‘file’ in memory The destination buffer should be freed with free().

const char *splinetable_get_key(const struct splinetable *table, const char *key)¶: Get the specified FITS header key as a C string.

int splinetable_read_key(const struct splinetable *table, splinetable_dtype type, const char *key, void *result)¶

Read a FITS header key

Parameters

[in] type – the type of the value
[in] key – the key
[out] result – where to store the result

int splinetable_convolve(struct splinetable *table, const int dim, const double *knots, size_t n_knots)¶

Convolve with another spline

Parameters

[in] dim – dimension to convolve
[in] knots – knot vector of convolution kernel
[in] n_knots – size of kernel knot vector

void splinetable_free(struct splinetable *table)¶: Destroy spline table.

Spline evaluation¶

int tablesearchcenters(const struct splinetable *table, const double *x, int *centers)¶

Find the indices of the central splines at coordinates x

Parameters

[in] x – coordinates
[out] centers – indices of central splines

Returns

0 if is within the partial support of the spline

double ndsplineeval(const struct splinetable *table, const double *x, const int *centers, int derivatives)

Evaluate the spline surface at coordinates x, with optional single differentiation

Parameters

[in] x – coordinates at which to evaluate
[in] centers – indices of the central splines
[in] derivatives – bitmask indicating which dimensions to differentiate

Pre

centers has been filled via a call to tablesearchcenters()

Returns

the value of the spline surface (or one of its derivatives) at x

void ndsplineeval_gradient(const struct splinetable *table, const double *x, const int *centers, double *evaluates)¶

Evaluate the spline surface and its gradient at coordinates x

Parameters

[in] x – coordinates at which to evaluate
[in] centers – indices of the central splines
[in] evaluates – storage for the evaluate and gradient (must have length at least ndim+1)

Pre

centers has been filled via a call to tablesearchcenters()

Photospline¶

Fitting tutorial (Python)¶

Fitting tutorial (C++)¶

Python library reference¶

C++ library reference¶

C library reference¶

Spline table I/O and manipulation¶

Spline evaluation¶

Table of Contents

This Page